Przez wiele lat domyślą funkcją aktywacji dla sieci konwolucyjnych było ReLU.

$$ReLU(x) = max(0,x)$$

Powodów było kilka:

• funkcja jest ekstremalnie prosta, przez co szybka w wywołaniu
• ma tylko jedną niezerową pochodną
• eksperymentalnie daje wyniki lepsze niż inne, powszechne fukcje aktywacji (tanh, sigmoid)

Te wcześniej, powszechnie używane funkcje dawały dobrą nieliniowość

$$sigmoid(x) = \frac{1}{1+e^{-x}}$$

$$tanh(x) = \frac{2}{1+e^{-2x}} - 1$$

będąc jednocześnie niezmiernie podobne, bo istnieje pomiędzy nimi proste przekształcenie:

$$tanh(x) = 2*sigmoid(2x)-1$$

Praca "Mish: A Self Regularized Non-Monotonic Neural Activation Function" proponuje nową funkcję, wszczynając przy tym dyskusję co to znaczy "dobra funkcja aktywacji".

Definicja

$$Mish(x) = x * tanh(ln(1+e^x))$$

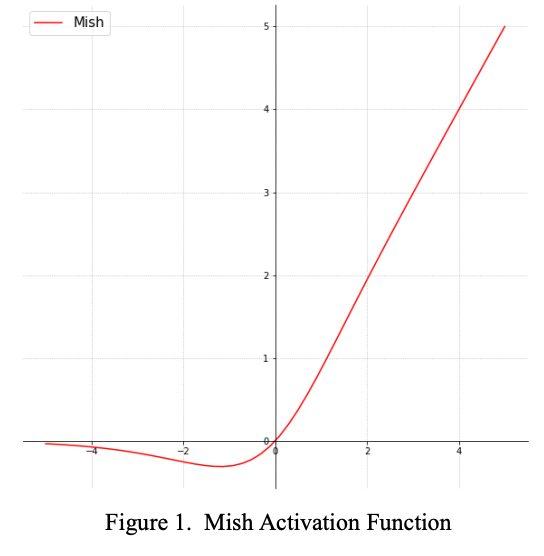
Funkcja ma cechy:

• nie jest monotoniczna
• jej pochodna nie jest monotoniczna
• aproksymacja przy zerze to f(x) = x

Funkcja, w odróżnieniu od ReLU jest gładka co wpływa na obraz przestrzeni na wyjściu funkcji:

Rezultaty

Autorzy chwalą się, że statystycznie sieci używające Mish charakteryzują się mniejszym błędem oraz mniejszym odchyleniem standardowym błędu niż przy użyciu innych funkcji.

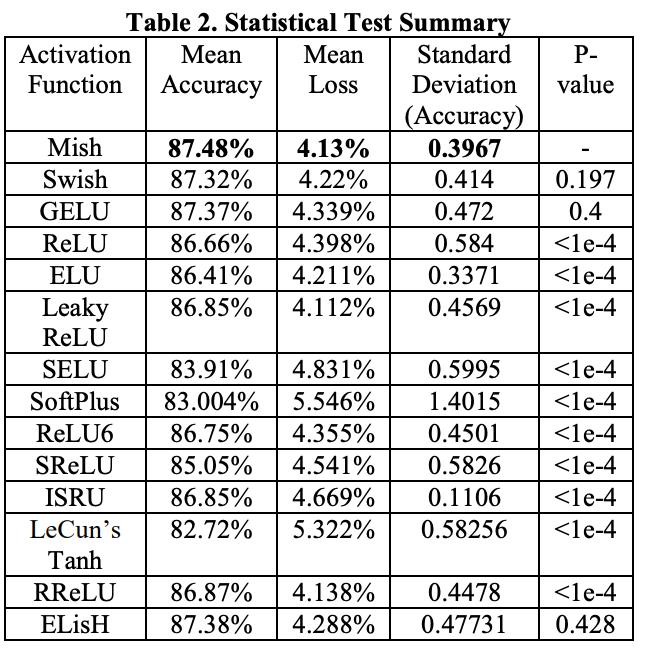
Wyniki klasyfikacji (TOP-1) na zbiorze CIFAR-10 dla różnych architektur sieci to odpowiednio:

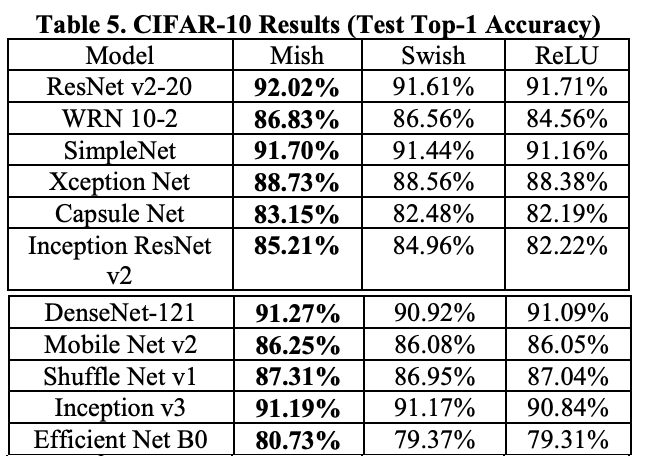
Głębsze sieci

Ciekawą obserwacją jest też zachowanie Accuracy (tutaj na zbiorze MNIST) przy użyciu rożnych funkcji aktywacji  w zależności od liczby warstw w pełni połączonych (fully connected):

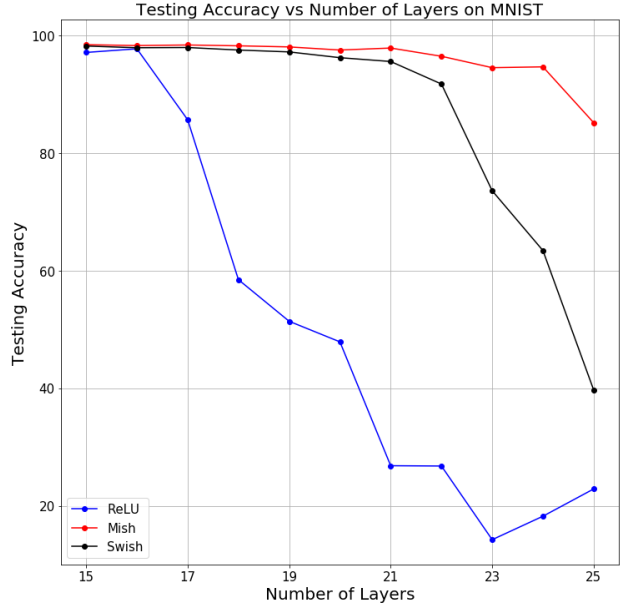
Funkcja Mish, będąc bardziej "gładka" pozwala na propagacje informacji do dalszych warstw sieci.

Implementacja

Implementacja funkcji aktywacji w PyTorch jest prosta, oto ona:

import torch
import torch.nn as nn
import torch.nn.functional as F  

class Mish(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, x):
        return x * (torch.tanh(F.softplus(x)))

Zapraszam do eksperymentowania!